Polymorphism
Introduction
Polymorphism is often seen as a characteristic unique to Object Oriented Programming (OOP) or at least one that it thrives in. Many have only seen polymorphism through the lens of an object oriented language and have yet to see other approaches to defining common interfaces.
I'll be using Java and Standard ML (SML) to demonstrate the various types of polymorphism. Java is unique in its pervasiveness throughout professional developers and its usage as a language to teach OOP. SML is unique in that it is a successor to one of the first implementations of a form of polymorphism different from the one used in OOP languages. More on that later.
Subtyping
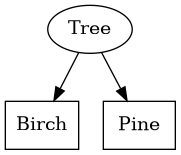
Subtyping Polymorphism is the form you're likely familiar with and were first introduced to. If we define a type \(T\) with a subtype \(S\), denoted as \(S <: T\), any operation that is well defined for \(T\) is also well defined for \(S\). For example, an interface to implementation class relationship in Java:
|
|
We define a common interface that all subtypes of Tree types will implement.
These new subtypes, Birch and Pine, will have their own implementation of
isDeciduous and sayBarkColor. In doing this, we don't have to know exactly what
tree we are working with, only that it is a subtype of Tree (as long as we
remain within the common operations of the interface type).
SML has a similar notion to this in its module system.
| Java | SML |
|---|---|
| interface | signature |
| class | structure |
We define a signature for a Tree similarly:
|
|
And make a Birch structure like:
|
|
Ad Hoc Polymorphism
Ad Hoc polymorphism is also likely something you're familiar with. Operations that are defined for different types may overload the function and perform different operations based on the types. Take for example, addition overloaded for various types:
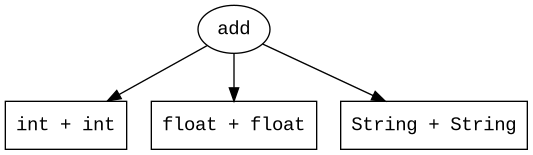
|
|
As you can see, add can now be used with int, float, or String without needing
to specify which add function to use.
As a programmer, we have to do more leg work to define the body of each
implementation of this interface, but it's easier to map a function's semantics to
a name mentally. Without ad hoc polymorphism, you may see function names like
add_ints and add_floats.
Also, notice how the functions are not restricted beyond requiring a certain
return type. The float addition function could return 0.0 in every case or
worse, it could modify global state without us knowing.
Ad hoc polymorphism put simply, is having the same function name but many different function bodies.
Parametric Polymorphism
Parametric polymorphism allows us to write a single function that applies to all
types. In SML, the "all types" concept is displayed through a letter prepended
with an apostrophe (commonly called "tick") such as 'a or 'b. Further, 'a must
be the same type as all other 'a in the function, but could be either the same
or different from 'b.
The function type is shown as an arrow in SML, so a function that accepts an int
and outputs an int may be written as int -> int. Let's define a function that
fulfills this type signature as an example.
|
|
val plus_one = fn : int -> int
We can also let SML infer the type of parameters by leaving out type annotations.
|
|
val plus_one = fn : int -> int
Now that we have this in mind, consider the case of appending two lists. The
list type is all that matters, not the type of list's content. So intuitively
we shouldn't have to define a new append for an int list and a bool list. Let's
try to define append and see the type that SML gives us for our function.
|
|
val append = fn : 'a list -> 'a list -> 'a list
Written mathematically, the type of append is
\begin{equation*} ∀ a . a \texttt{ list} → a \texttt{ list} → a \texttt{ list} \end{equation*}
Telling us that we can apply this to any two lists, as long as the two lists have the same type. Great! That matches our expectations. Let's consider a version with multiple polymorphic types. Consider swapping a tuple (or pair) of elements. Again, we don't need to know the types of the elements inside the tuple. And in this example, it doesn't matter if the pair has two elements of the same type or different.
|
|
val swap = fn : 'a * 'b -> 'b * 'a
Or, mathematically:
\begin{equation*} ∀ a ∀ b . a × b → b × a \end{equation*}
Parametric polymorphism allows us to write generic functions that apply to many types and all share the same body - thereby saving us from implementing a case for each type. However, perhaps obviously, the functions that can be implemented for every type are not able to use any operation limited to a type. For example, we could not add, check equality, or use an xor op on a parameter without limiting our type. Some systems
Parametric polymorphism been implemented in Java through generics.
Comparison
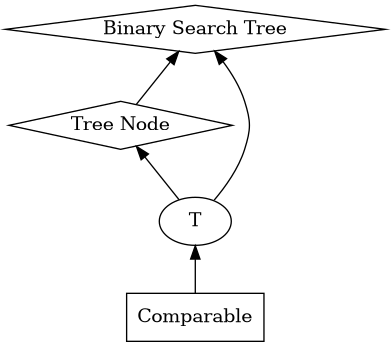
Let's put all this new knowledge to the test by making a polymorphic binary search tree. This will require all forms of polymorphism that we've seen to make work.
Java
|
|
We specify that the included value must have or extends a class that is
Comparable so that we may ensure ordering in the tree. But, we need to define
this class too.
|
|
|
|
1 5 100
SML
How do we achieve this in SML? When we covered parametric polymorphism, we saw that using things such as equality and comparison would restrict our type. In SML, we can use what's called a functor to make a structure which is parametrized another structure. This allows us to compose structures and implement a generic binary search tree.
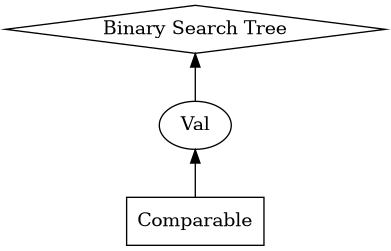
We define a module that implements comparison between its type, similar to how
Comparable in java works. While we're at it, let's define a more informative
return type for comparison than the signedness of an integer.
|
|
Then we may make the functor and require a parameter for the inner type.
|
|
We need to define a structure that fulfills the signature of COMPARABLE.
|
|
Then we can pass it into our BinarySearchTree functor.
|
|
And now we can use our new binary search tree.
|
|
1 5 100